Date published: 2018-05-01
Mercury’s crust revisited
In today’s volume of the “Earth and Planetary Science Letters”, Michael M. Sori from the “Lunar and Planetary Laboratory” of the University of Arizona (US) writes about how he used data obtained with the MESSENGER (Mercury Surface, Space Environment, Geochemistry and Ranging) orbiter to re-measure the crust thickness of Mercury. Crust thickness is an important geophysical parameter, which allows to further constrain terrestrial planet formation scenarios. And since Mercury is always good for a surprise, the new calculations show that Mercury’s crust is only 26±11 km thick, i.e. much thinner (and also denser) than previously thought.
First estimates of the Mercury crust thickness were published by Anderson et al. (1996). Their estimates were based on data obtained with the Mariner 10 spacecraft. They concluded that the crust is 100–300 km thick. Almost ten years later, with a wealth of new instruments on-board MESSENGER to create gravity and topography maps, Padovan et al. (2015) concluded that Mercury’s crustal thickness is on average 35±18 km. The authors assumed topography was predominantly compensated by Airy isostasy, where columns contain equal masses. The equal mass approach was now shown to overestimate the thickness of Mercury’s crust, and instead an equal pressure approach (first described by Hemingway and Matsuyama 2017) should be used. In the next paragraphs, further explanations follow, describing the meaning of isostasy and the equal-mass vs. equal-pressure approaches.
Airy vs. Pratt isostasy and the “equal mass” vs. “equal pressure” assumptions
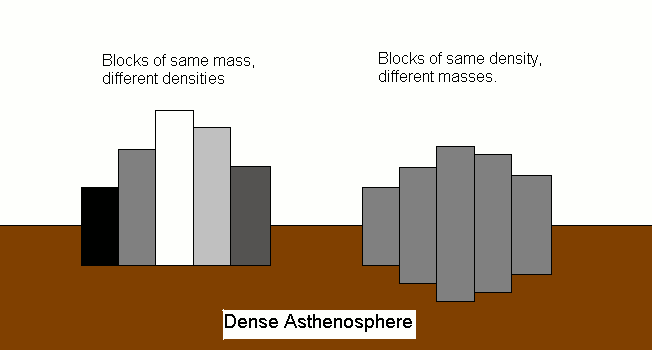
Isostasy is a fundamental concept in Geology, meaning that lighter crust floats on the denser underlying mantle. It thus explains why mountains and valleys are stable over large timescales. This is called isostatic equilibrium (this equilibrium can be disturbed by erosion or volcanic activity). There are two main ideas how mountain masses are supported (see Figure 1). In Pratt’s theory, the density changes across the surface and less dense crustal blocks “float” higher, whereas the more dense blocks form basins. On the other side, in Airy’s theory the density is constant, but the crustal blocks have different thicknesses. Higher mountains have deeper “roots” into the denser material below. Thus, in case of Pratt isostasy, one would expect a correlation between density and elevation across the surface of a planet, with mountains having lower densities.
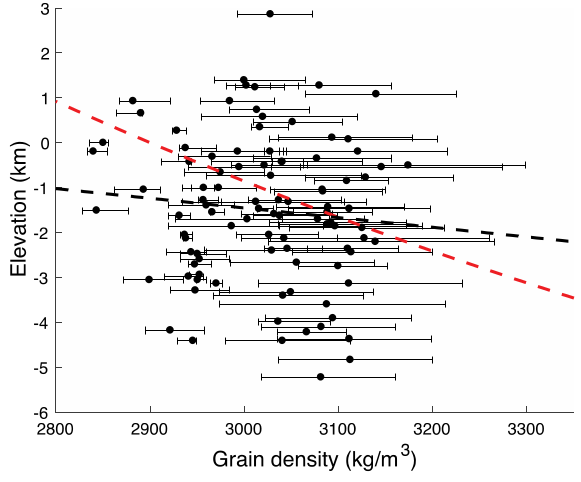
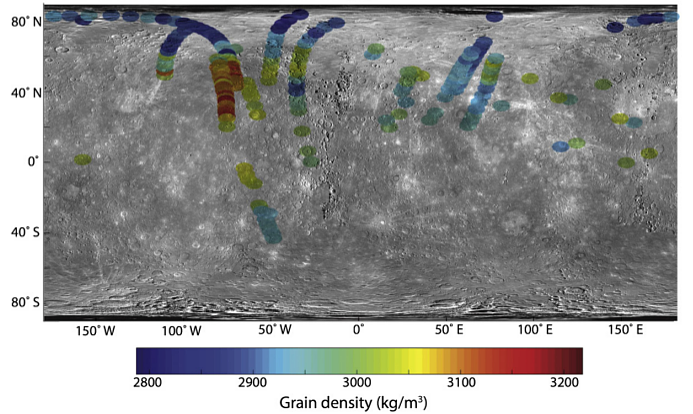
In the study, Sori (2018) shows grain density measurements across several regions of Mercury (see Figure 2). Using MESSENGER’s topography maps, the author could then look for a correlation between density and elevation. As shown in Figure 3, such a correlation does not exist. Thus, it can be assumed that Airy isostasy is a better description for the topography of Mercury.
Now we come back to the meaning of “equal mass” and “equal pressure” approach. The latter one was used by the author of the study. This is the crucial difference that finally led to the new lower value for the crustal thickness. First, it is important to know that the gravitational potential is typically not constant across topographic lines (=lines of constant altitude) of a planet. This is due to variations in density. However, lines of constant gravitational potential (equipotential lines) can still be calculated. One such line of constant gravitational potential is the zero-level (on Earth roughly the sea level) and is called geoid. The quantity called geoid-topography ratio (GTR) thus reflects variations in density. And finally, the GTR is used to calculate the thickness of the crust. The main question is how equipotential surfaces are calculated. As shown by Douglas J. Hemingway and Isamu Matsuyama (2017), the spherical geometry of the problem must be taken into account when calculating equipotential surfaces (which will affect the crust thickness calculation). And here is the problem. Previous publications have assumed a constant width of the crustal blocks (in cartesian coordinates). This is what is called the “equal mass” approach, but in fact one would need to take into account the spherical symmetry (polar coordinates) and thus cone-shaped blocks that put different “pressure” on the surface (compare Figure 1 and Figure 5). This is why the newly calculated thickness is roughly 25% lower than previous results. Note that, the same issue will also affect previous calculations of other objects in the solar system. However, since the difference is larger for smaller objects, Mercury is affected most of all planets, since it is the smallest planet in the solar system.
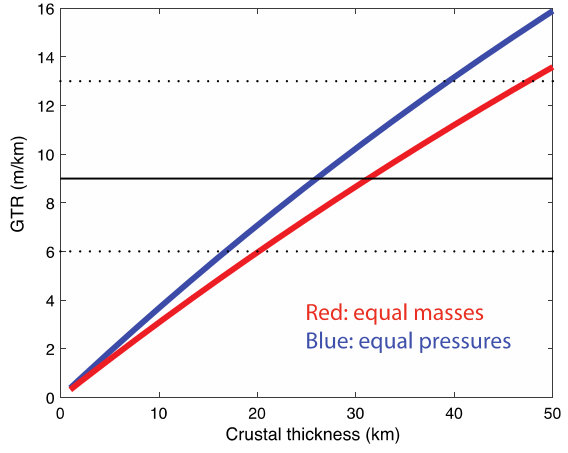

As explained, the equal pressure approach is a better representation of a state of equilibrium. This is also supported by the fact that the new average crustal thickness value of 26±11 km agrees well with other MESSENGER based models and observations, e.g. with Mercury’s crust being of magmatic origin or excavation of mantle material onto the surface, which was proposed by Padovan et al. (2015).
With this publication another issue of Mercury could be resolved, but many things are left unknown and Mercury still keeps scientist busy. The next large step forward is likely to come when BepiColombo finally orbits Mercury in 2025.
