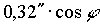3.1 Allgemeines
Zur Ephemeridenrechnung sind folgende Schritte nötig:
- Umwandlung des gewünschten Datums des Julianischen Kalenders in die entsprechende Julianische Tageszahl
- Berechnen der heliozentrischen ekliptikalen Koordinaten mit Hilfe der VSOP87 – Theorie
- Transformation zu geozentrischen ekliptikalen Koordinaten (geometrische Position)
- Transformation zu geozentrischen äquatorialen Koordinaten (scheinbare Position)
3.2 Umwandlung eines Datums des Julianischen Kalenders in die Julianische Tageszahl
JD: Julianischer Tag
Y: Jahr
M: Monat
D: Tag
UT: Weltzeit (Universal Time UT)
Vorerst müssen einige Hilfsgrößen (y, m, B) berechnet werden:
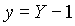 |
UND | 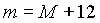 |
falls M 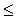 2 2 |
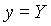 |
UND | 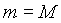 |
falls M > 2 |
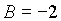 |
bis einschließlich 04.10.1582 |
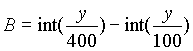 |
ab einschließlich 15.10.1582 |
Die Formel zur Bestimmung des Julianischen Tages lautet:
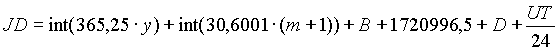
Beispiel: 29. 11. 1998, 0h
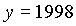 |
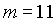 |
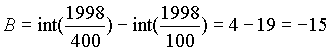 |
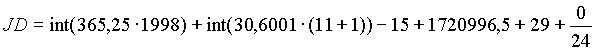
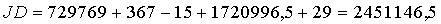
Beispiel: 23. 02. 1893, 0h
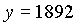 |
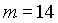 |
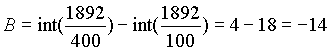 |
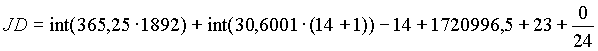
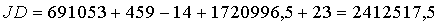
Beispiel: 07. 10. 1312, 0h
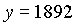 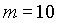 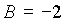 |
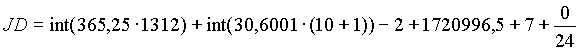
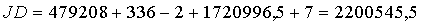
3.3 Berechnung der heliozentrischen ekliptikalen Koordinaten mit Hilfe der VSOP87
P. Bretagnon und Francou veröffentlichten 1987 die Planetentheorie VSOP87 zur direkten Berechnung der heliozentrischen ekliptikalen Koordinaten. Die VSOP87 (“Variations Séculaires des Orbites Planétaires”) besteht aus langen Reihen periodischer Terme für die Planeten Merkur bis Neptun.
Im Anhang lassen sich die Reihen für Venus und Erde wiederfinden, wobei die Terme gekürzt wurden. Somit ergeben sich Ungenauigkeiten in den berechneten Koordinaten, welche jedoch unbedeutend klein sind. Hat man jedoch die gesamte Theorie zur Hand, kann das im weiteren beschriebene Schema zur Berechnung der Koordinaten genauso angewandt werden. Die VSOP87 liefert also:
l: heliozentrische ekliptikale Länge
b: heliozentrische ekliptikale Breite
r: Entfernung von der Sonne
Die Reihen für jeden einzelnen Planeten sind unterteilt: (siehe Anhang)
- Reihen unter der Bezeichnung L0, L1, L2, … werden zur Berechnung der heliozentrischen ekliptikalen Länge gebraucht.
- Reihen unter der Bezeichnung B0, B1, B2, … werden zur Berechnung der heliozentrischen ekliptikalen Breite gebraucht.
- Reihen unter der Bezeichnung R0, R1, R2, … werden zur Berechnung des Sonnenabstands gebraucht.
Jede Reihe besteht aus einzelnen Termen: (siehe Anhang)
Unter einem Term versteht man 3 Zahlen (A, B, C), welche horizontal angelegt sind, und der Wert eines einzigen Terms ist folgendermaßen definiert:
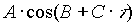
wobei:
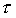 : Dies ist die Zeit, welche in Julianischen Jahrtausenden von der Standardepoche J2000 (1. Januar 2000 12h; in Julianischen Tagen: 2451545,0) ausgehend, angegeben wird.
: Dies ist die Zeit, welche in Julianischen Jahrtausenden von der Standardepoche J2000 (1. Januar 2000 12h; in Julianischen Tagen: 2451545,0) ausgehend, angegeben wird.
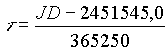
- A: Dies sind Koeffizienten, die in Einheiten von 10-8 rad bei ekliptikaler Länge und Breite gegeben sind. Bei der Entfernung r (Sonne – Erde) sind diese Koeffizienten in 10-8 AE gegeben.
- B, C: Größen, die im Bogenmaß angegeben sind.
Um die heliozentrische ekliptikale Länge, Breite und die Entfernung Sonne – Erde zu erhalten, geht man folgendermaßen vor:
Man berechne die Summe der Werte jedes einzelnen Terms von Reihe L0, die Summe der Werte jedes einzelnen Terms von Reihe L1 usw. Dann ist die gesuchte heliozentrische ekliptikale Länge in Bogenmaß gegeben durch:
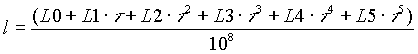
In der gleichen Weise verfahre man mit den Termen und Reihen für die heliozentrische ekliptikale Breite (B0, B1, B2, …) und den Termen und Reihen für die Entfernung Sonne – Planet (R0, R1, R2, …).
Beispiel: heliozentrische ekliptikale Koordinaten für Venus am 20. 12. 1992, 0h
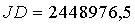
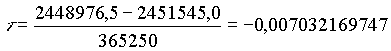
z. B.: Summe der Reihe L2:
| Wert des 1. Terms der Reihe L2: | +54127,00000000000000000000000000000 |
| Wert des 2. Terms der Reihe L2: | -2765,68914432686125597362190306098 |
| Wert des 3. Terms der Reihe L2: | -1295,95811507646894393548388015404 |
| Wert des 4. Terms der Reihe L2: | -6,96070676738931515453944825754 |
| Wert des 5. Terms der Reihe L2: | -2,51593284332098056645989120796 |
| Wert des 6. Terms der Reihe L2: | +0,87097547092903710795233000817 |
| Wert des 7. Terms der Reihe L2: | -6,92415079707988424352932014731 |
| Wert des 8. Terms der Reihe L2: | +5,64379188984989445657219331589 |
| SUMME L2: | +50055,46671754965855169089008049730 |
Dies auf alle anderen Reihen (L0, L1, L3, L4, L5) der Venus angewandt, ergibt:
| L0 = +316402122 | L3 = -56 |
| L1 = +1021353038718 | L4 = -109 |
| L2 = +50055 | L5 = -1 |
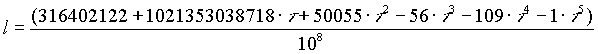
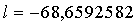 rad = -3933°,88572 = +26°,11428
rad = -3933°,88572 = +26°,11428
Somit betrug die heliozentrische ekliptikale Länge der Venus am 20. 12. 1992, 0h +26°,11428.
In der gleichen Weise verfahre man mit den Termen und Reihen für die heliozentrische ekliptikale Breite (B0, B1, B2, …) und den Termen und Reihen für die Entfernung Sonne – Planet (R0, R1, R2, …). Dadurch ergeben sich folgende Werte:
| b = -0,0457399 rad = -2°,62070 | r = 0,724603 AE |
3.4. Transformation zu geozentrischen ekliptikalen Koordinaten (geometrische Position)
Um die heliozentrischen ekliptikalen Koordinaten (l, b, r) eines Planeten in die geozentrischen ekliptikalen Koordinaten (x, y, z) transformieren zu können, müssen vorerst die heliozentrischen ekliptikalen Koordinaten der Erde (l0, b0, r0) mit der in Kapitel 3.3. beschriebenen Methode errechnet werden.
Sind diese schließlich bekannt, kann die Transformation der heliozentrischen ekliptikalen Koordinaten – sphärische Darstellung – in geozentrische ekliptikale Koordinaten – kartesische Darstellung durchgeführt werden: (siehe Kapitel 2.1.)
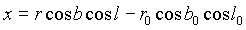
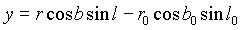
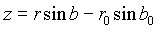
Die so ermittelten geozentrischen ekliptikalen Koordinaten in kartesischer Darstellung (x, y, z) lassen sich nun in die sphärische Darstellung (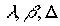 ) transformieren. (siehe Kapitel 2.1.)
) transformieren. (siehe Kapitel 2.1.)
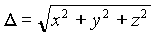
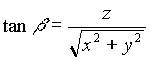
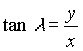
Beispiel: geozentrische ekliptikale Koordinaten für Venus am 20. 12. 1992, 0h
Die zuvor schon berechneten heliozentrischen ekliptikalen Koordinaten der Venus lauten:
| l: +26°,11428 | b: -2°,62070 | r: 0,724603 AE |
Es ergeben sich für die heliozentrischen ekliptikalen Koordinaten für die Erde am 20. 12. 1992, 0h:
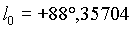 |
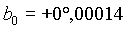 |
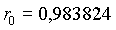 AE AE |
Die Transformation zu geozentrischen ekliptikalen Koordinaten (kartesisch) ergibt:
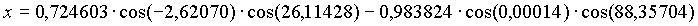
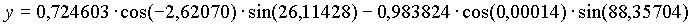
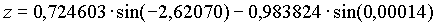
Die geozentrischen ekliptikalen Koordinaten (kartesisch dargestellt) für die Venus am 20. 12. 1992, 0h waren also:
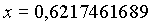
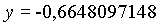
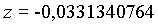
Die geozentrischen ekliptikalen Koordinaten in sphärischer Darstellung sind danach:
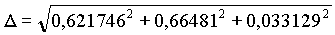
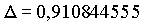 AE
AE
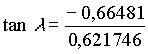
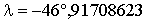
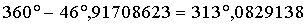
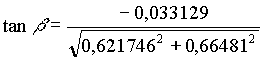
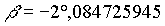
3.5 Transformation zu geozentrischen äquatorialen Koordinaten (scheinbare Position)
Zur Berechnung der geozentrischen äquatorialen Koordinaten, muß vorerst die Schiefe der Ekliptik (Neigung der Rotationsachse der Erde = Winkel zwischen Ekliptik und Himmelsäquator) zum gewünschten Zeitpunkt 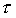 bekannt sein, wobei
bekannt sein, wobei 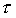 diesmal in Julianischen Jahrhunderten von der Standardepoche J2000,0 (1. Januar 2000, 12h; in Julianischen Tagen: 2451545,0) gemessen, angeben werden muß. Somit gilt für
diesmal in Julianischen Jahrhunderten von der Standardepoche J2000,0 (1. Januar 2000, 12h; in Julianischen Tagen: 2451545,0) gemessen, angeben werden muß. Somit gilt für 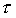 :
:
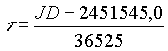
Die mittlere Schiefe der Ekliptik (durch Internationale Astronomische Union festgelegt) zum Zeitpunkt 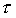 durch:
durch:
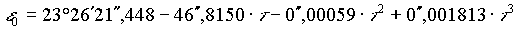
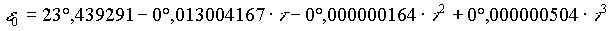
Die geozentrischen äquatorialen Koordinaten sind nun folgendermaßen gegeben:
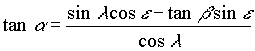
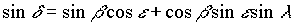
Beispiel: geozentrische äquatoriale Koordinaten für Venus am 20. 12. 1992, 0h
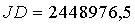
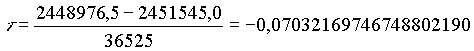
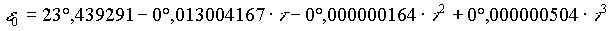
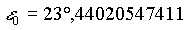
Die zuvor schon berechneten geozentrischen ekliptikalen Koordinaten für die Venus am 20. 12. 1992, 0h lauten:
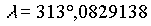 |
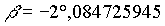 |
Die geozentrischen äquatorialen Koordinaten für die Venus am 20. 12. 1992, 0h waren also:
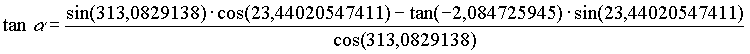
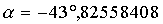
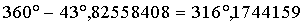
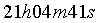
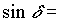
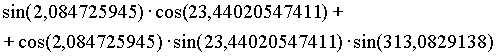
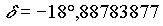
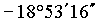
3.6 Genauigkeit der Ergebnisse:
Falls das in meiner Arbeit beschriebene Schema zur Ephemeridenrechnung mit der gesamten Planetentheorie VSOP87 angewandt wird, ergeben sich Abweichungen durch folgende Effekte: (siehe Kapitel 2.2.)
- Nutation und Schiefe der Ekliptik
- Lichtlaufzeit und Aberration
Nutation und Schiefe der Ekliptik:
In meiner Arbeit beziehen sich die Koordinaten auf die mittlere Schiefe der Ekliptik, welche von der Internationalen Astronomischen Union festgelegt wurde. Der Fehler in der mittleren Schiefe der Ekliptik 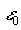 gegenüber der wahren Schiefe der Ekliptik erreicht über einen Zeitraum von 2000 Jahren
gegenüber der wahren Schiefe der Ekliptik erreicht über einen Zeitraum von 2000 Jahren 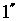 und über einen Zeitraum von 4000 Jahren
und über einen Zeitraum von 4000 Jahren 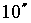 .
.
Lichtlaufzeit und Aberration:
Die Abweichung zwischen scheinbarer und wahrer Richtung zu einem Planeten bedingt durch die jährliche Aberration ist sehr gering, denn die Erdgeschwindigkeit (ca. 30 km/s) ist sehr klein gegen die Lichtgeschwindigkeit c (ca. 300 000 km/s).
Die Abweichung zwischen scheinbarer und wahrer Richtung zu einem Planeten bedingt durch die tägliche Aberration ist abhängig von der Position des Beobachters auf der Erde (abhängig von der geographischen Breite 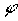 ). Für einen Beobachter an einem der Pole fällt die Abweichung weg (0° Abweichung). Am Äquator jedoch ist sie am größten (
). Für einen Beobachter an einem der Pole fällt die Abweichung weg (0° Abweichung). Am Äquator jedoch ist sie am größten (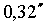 ), denn für die tägliche Aberration gilt:
), denn für die tägliche Aberration gilt: