2.1 sphärische und kartesische Darstellung
Um den Ort eines Punktes im Raum zu beschreiben, wird ein Koordinatensystem benötigt, welches durch einen Nullpunkt, eine Bezugsrichtung und eine Bezugsebene festgelegt ist. Es gibt zwei verschiedene Möglichkeiten zur Auffindung eines Punktes in einem solchen Koordinatensystem:
A) Angabe in kartesischen (rechtwinkligen) Koordinaten
B) Angabe in sphärischen Koordinaten (Polarkoordinaten)
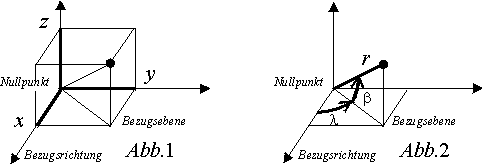
ad A) kartesische (rechtwinklige) Koordinaten: (siehe Abb. 1)
Die Koordinaten eines Punktes werden in der Form (x, y, z) angegeben, welche die Längen der Projektionen des Punktes auf die entsprechenden Achsen wiedergeben.
ad B) sphärische Koordinaten (Polarkoordinaten): (siehe Abb. 2)
Die Koordinaten eines Punktes werden in der Form (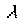 ,
,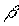 ) angegeben, wobei
) angegeben, wobei 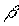 als Breite bezeichnet wird und den Winkel zwischen der Bezugsebene und der Verbindung Nullpunkt – Punkt angibt.
als Breite bezeichnet wird und den Winkel zwischen der Bezugsebene und der Verbindung Nullpunkt – Punkt angibt. 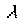 wird als Länge bezeichnet und gibt den Winkel zwischen der Projektion der Verbindung Nullpunkt – Punkt auf die Bezugsebene und der Bezugsrichtung an. Der Abstand des Punktes vom Nullpunkt wird als r bezeichnet.
wird als Länge bezeichnet und gibt den Winkel zwischen der Projektion der Verbindung Nullpunkt – Punkt auf die Bezugsebene und der Bezugsrichtung an. Der Abstand des Punktes vom Nullpunkt wird als r bezeichnet.
| sphärisch – kartesisch | kartesisch – sphärisch |
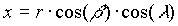 |
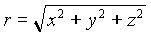 |
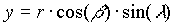 |
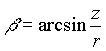 |
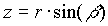 |
 |
Die Winkel sind alle im Gradmaß gemessen und es wird vorausgesetzt, daß sich beide Systeme auf den selben Nullpunkt, die selbe Bezugsrichtung und die selbe Bezugsebene beziehen.
2.2 verwendete Begriffe
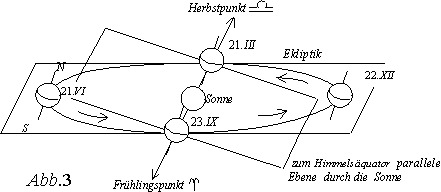
Ekliptik: (siehe Abb. 3)
Betrachtet man die Bahn der Erde um die Sonne, so stellt man fest, daß alle Punkte dieser Bahn in einer Ebene liegen, die durch die Mitte der Sonne geht (= Ekliptik).
Himmelsäquator: (siehe Abb. 3)
Legt man eine Ebene durch den Erdmittelpunkt, die senkrecht auf der Erdachse steht, schneidet diese die Erdoberfläche im Erdäquator (= Himmelsäquator).
Frühlingspunkt, Herbstpunkt: (siehe Abb. 3)
Legt man eine Ebene durch den Sonnenmittelpunkt, die parallel zur Himmelsäquatorebene liegt, dann schneidet sich diese mit der Ekliptik in einer Gerade, die wieder durch die Sonne geht. Die Richtungen, in die diese Gerade zeigt, bezeichnet man als Frühlingspunkt (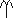 ) und Herbstpunkt (
) und Herbstpunkt (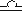 ).
).
aufsteigender Knoten:
Als aufsteigender Knoten wird jener Punkt bezeichnet, in dem ein Planet die Ekliptik von Süden nach Norden – also “aufsteigend” – durchstößt.
Äquinoktium:
Da Himmelsäquator und Ekliptik über lange Zeiträume hinweg, nicht fest im Raum stehen, sondern eine Bewegung durchmachen, welche als Präzession bezeichnet wird, muß der Zeitpunkt bekannt sein, auf welchen sich die Angaben der Koordinaten beziehen. So bedeutet etwa “Äquinoktium 2000.0”, daß sich die Koordinaten auf die Lage von Himmelsäquator, Ekliptik und Frühlingspunkt des 1. Januars, 12h des Jahres 2000 beziehen.
Präzession:
Die Neigung des Erdäquators gegen die Ekliptik liegt bei ca. 23°27′ (Schiefe der Ekliptik). Somit ist der Erdäquatorwulst nicht auf die Sonne ausgerichtet. Folglich übt die Sonne ein Drehmoment auf den Erdäquatorwulst aus, welches die Aufrichtung der Erdachse bewirkt. Außerdem liegt die Mondbahnebene in etwa auf der Ekliptik und so übt auch dieser ein Drehmoment auf den Erdäquatorwulst aus. Da die Erde durch die Rotation um die eigene Achse einen Kreisel darstellt, muß sie den physikalischen Gesetzen zufolge, rechtwinklig ausweichen (= Präzession).
Nutation und Schiefe der Ekliptik:
Der Präzession überlagert ist die Nutation. Diese entsteht durch den unterschiedlich großen Einfluß des Mondes auf den Erdäquatorwulst. Der Einfluß des Mondes erreicht ein Minimum, wenn der Winkel zwischen der Mondbahnebene und dem Erdäquator am kleinsten ist, und ein Maximum, wenn dieser Winkel am größten ist. Die Nutation verursacht somit eine Änderung in der Schiefe der Ekliptik (Neigung der Rotationsachse der Erde = Winkel zwischen Ekliptik und Himmelsäquator).
Lichtlaufzeit und Aberration:
Diese zwei Effekte sind verantwortlich für die scheinbare Ortsveränderung eines Planeten:
- Lichtlaufzeit: der Planet wird dort gesehen, wo er war, als der Lichtstrahl ihn verließ (aufgrund endlicher Geschwindigkeit des Lichts).
- Aberration: durch die Bewegung der Erde um die Sonne (jährliche Aberration) und um die eigene Achse (tägliche Aberration), verändert sich die Einfallsrichtung des Lichts.
Julianische Tageszahl (Julianischer Tag):
Dies ist eine fortlaufende Zählung von Tagen und deren Bruchteilen vom Beginn des astronomischen Jahres -4712. Das astronomische Jahr -4712 entspricht dem Jahr 4713 v. Chr. (christliche Zeitzählung). Das astronomische Jahr 0 entspricht also dem Jahr 1 v. Chr. In der christlichen Zeitzählung gibt es jedoch das Jahr 0 nicht und es folgt das Jahr 1 n. Chr., welches somit dem astronomischen Jahr 1 entspricht. Folgend ist die Tageszahl der astronomischen Zeitzählung gleich der Tageszahl der christlichen Zeitzählung.
Bis zum 4. Oktober 1582 n. Chr. galt der Julianische Kalender, demzufolge in jenen Jahren ein 29. Februar als Schalttag eingeführt wurde, deren astronomische Jahreszahl durch vier teilbar war.
Bis zum Mittag des 4. Oktobers 1582 – zu beachten ist, daß der Julianische Tag um 12h Weltzeit (Universal Time UT) beginnt – waren also 2 299 160,0 Julianische Tage vergangen.
Die gregorianische Kalenderreform ließ auf diesen Tag sofort den 15. Oktober 1582 folgen, dessen Beginn somit der Julianischen Tageszahl 2 299 160,5 entspricht. Seit diesem Zeitpunkt ist jedes Jahr ein Schaltjahr, dessen Jahreszahl
- durch vier, aber nicht durch hundert teilbar ist oder
- durch vierhundert teilbar ist.
2.3 Heliozentrisch – ekliptikales Koordinatensystem
- Nullpunkt: Sonne
- Bezugsebene: Ekliptik
- Bezugsrichtung: Frühlingspunkt
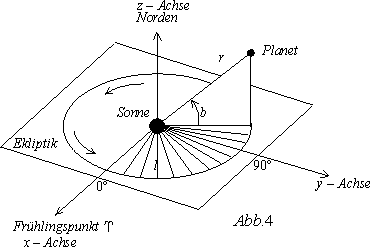
- r: Entfernung von der Sonne
- b: ekliptikale Breite:
- Der Winkel zwischen der Linie Sonne – Planet und der Ekliptik. Gemessen wird dieser von der Ekliptik aus gesehen nach Norden positiv und nach Süden negativ.
- ekliptikale Länge:
- Der Winkel zwischen dem Frühlingspunkt und der Projektion der Linie Sonne – Planet auf die Ekliptik. Gemessen wird dieser vom Frühlingspunkt aus gesehen in Richtung der Erdbewegung von 0° bis 360°.
2.4 Geozentrisch – ekliptikales Koordinatensystem
- Nullpunkt: Erdmittelpunkt
- Bezugsebene: Ekliptik
- Bezugsrichtung: Frühlingspunkt
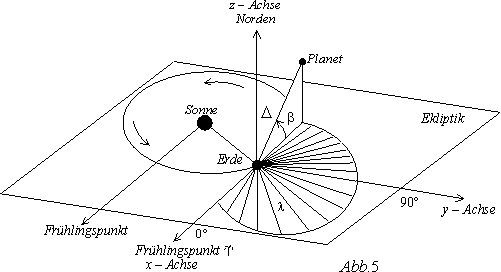
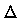 :Entfernung von der Erde
:Entfernung von der Erde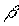 :ekliptikale Breite:
:ekliptikale Breite:
- Der Winkel zwischen der Linie Erde – Planet und der Ekliptik. Gemessen wird dieser von der Ekliptik aus gesehen nach Norden positiv und nach Süden negativ.
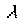 :ekliptikale Länge:
:ekliptikale Länge:
- Der Winkel zwischen dem Frühlingspunkt und der Projektion der Linie Erde – Planet auf die Ekliptik. Gemessen wird dieser vom Frühlingspunkt aus gesehen in Richtung der Erdbewegung von 0° bis 360°.
2.5 Geozentrisch – äquatoriales Koordinatensystem
- Nullpunkt: Erdmittelpunkt
- Bezugsebene: Himmelsäquator
- Bezugsrichtung: Frühlingspunkt
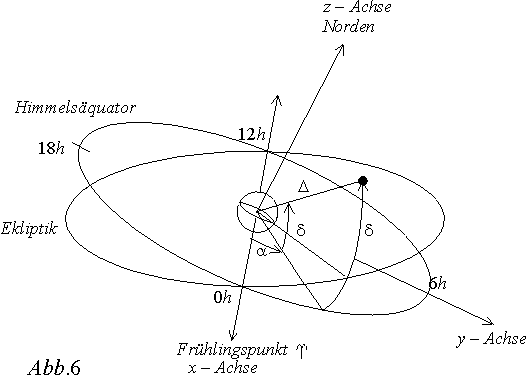
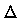 :Entfernung von der Erde
:Entfernung von der Erde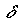 :Deklination:
:Deklination:
- Der Winkel zwischen der Linie Erde – Planet und dem Himmelsäquator. Gemessen wird dieser vom Himmelsäquator aus gesehen nach Norden positiv und nach Süden negativ.
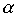 :Rektaszension:
:Rektaszension:
- Der Winkel zwischen dem Frühlingspunkt und der Projektion der Linie Erde – Planet auf den Himmelsäquator. Gemessen wird dieser vom Frühlingspunkt aus gesehen in Richtung der Erdbewegung von 0h bis 24h.